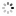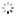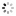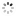Important Collectors’ Wristwatches, P...

New York - The Fuller Building, Jun 14, 2007

LOT 219

"Los Angeles - Equation of Time" Audemars Piguet, Genève, "Jules Audemars - Sunrise - Sunset - Equation du Temps", No. 548523, case No. E 66104, Ref. 2599 BA. Made in a limited quantity each year since 2000. Very fine and important, astronomic, self-winding, water-resistant, diamond-set 18K yellow gold gentleman's wristwatch with perpetual calendar, leap year, moon phases, sunrise and sunset set for Los Angeles, equation of time, 40-hour autonomy and an 18K yellow gold Audemars Piguet deployant clasp. Accompanied by a fitted box, setting pin and certificate.

USD 40,000 - 50,000

EUR 30,000 - 37,000

Sold: USD 44,840

C. Three-body, solid, polished, entirely set with a total of 299 round diamonds, transparent case back with 5 screws, engraved bezel with graduation for the equation of time (Los Angeles latitude of 11h 53'), straight lugs, sapphire crystals. D. Guilloché mother-of-pearl with applied yellow gold star indexes, each set with a round diamond, subsidiary plain mother-of-pearl dials for the days of the month, of the week at 6, 12-hour sunrise dial at 9 and 24-hour sunset dial at 3, aperture for the leap year at 1, the months and the aperture for the moon phases at 12. Black skeletonized "alpha" hands. M. Cal. 2120, rhodium-plated, "fausses côtes" decoration, 41 jewels, straight-line lever escapement, free-sprung Gyromax balance adjusted to heat, cold, isochronism and 5 positions, shock absorber, self-compensating flat balance spring, handengraved and skeletonized rotor with 21K gold segment. Dial, case and movement signed. Diam. 39 mm. Thickness 12 mm. Property of a West Coast Collector


LOADING IMAGES
Click to full view
Image
Grading System
Grade: AAA

Excellent
Case: 1

As new
Movement: 1

As new
Dial: 1-01

As new

HANDS Original

Notes

Equation of Time Equation of time indicates the time difference between the true solar day and the mean solar day (or time told by a clock or watch). It has 2 major causes: The first is that the plane of the Earth's Equator is inclined to Earth's orbital plane. The second is that the orbit of the Earth around the Sun is an ellipse and not a circle. Equation of Time due to Obliquity (the Earth's tilt): If the Earth's rotational axis was not tilted with respect to its orbit around the Sun, the apparent motion of the Sun along the Ecliptic would fall directly on the Equator, covering the same angles along the Equator in equal time. However, this is not the case, since the angular movement is not linear in terms of time, because it changes as the Sun moves above and below the Equator. The projection of the Sun's motion onto the Equator will be at a maximum, when its motion along the Ecliptic is parallel to the Equator (at the summer and winter solstices) and will be at a minimum at the equinoxes. Equation of Time due to Unequal Motion (the Earth's elliptical orbit): The orbit of the Earth around the Sun is an ellipse. The distance between the Earth and the Sun is at a minimum around December 31 and is greatest around July 1. The Sun's apparent longitude changes fastest, when the Earth is closest to the Sun. The Sun will appear on the meridian at noon on these two dates and so the Equation of Time due to Unequal Motion will then be zero. The mean solar day, calculated by averaging all the days of the year, was invented by astronomers for convenience so that the solar day would always be 24 hours. True solar time and mean solar time coincide four times a year, on April 16, June 14, September 1, and December 25. On these days, the equation will equal zero. During the other 361 days, the equation of time must be used to indicate the difference between the two times, amounting over 16 minutes at certain times of year. The minimum difference occurs on November 1 with a loss of 16 minutes and 23 seconds and the maximum occurs on February 11 with an increase of 14 minutes 20 seconds. This positive and negative value is offset in the time of the local noon and those of sunrise and sunset. Equation of time, often represented by a figure 8, called an "analemma", can be approximated by the following formula: E = 9.87 * sin (2B) - 7.53 * cos (B) - 1.5 * sin (B) Where: B = 360 * (N-81) / 365 Where: N = day number January 1 = day 1.