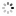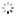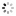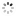Important Modern & Vintage Timepieces
Hong - Kong, Oct 09, 2010
LOT 299
Audemars Piguet Equation of Time Madrid Audemars Piguet, Genève, "Jules Audemars, Sunrise - Sunset - Equation du Temps", movement No. 505872, case No. E 50937. Made in a limited quantity each year since 2000. Very fine and important, astronomic, self-winding, water-resistant, 18K pink gold wristwatch with perpetual calendar, leap year, moon phases, sunrise and sunset adjusted for the city of Madrid, equation of time, 40-hour autonomy and an 18K pink gold Audemars Piguet deployant clasp. Accompanied by fitted winding box.
HKD 100,000 - 150,000
USD 13,000 - 20,000 / EUR 10,000 - 15,000
Sold: HKD 175,000
C. Three-body, solid, polished and brushed, transparent case back with 5 screws, engraved bezel with graduation for the equation of time and Madrid latitude of 13 h 55?, straight lugs, sapphire crystals. D. Two-tone guilloche silver with applied pink gold triangular and baton indexes, outer minute track with 5-minute Arabic markers on a plain reserve, subsidiary dials for the days of the month, of the week at 6, 12-hour sunrise dial at 9 and 24-hour sunset dial at 3, aperture for the leap year at 1, the months and aperture for the moon phases at 12. Black skeletonized alpha hands. M. Cal. 2120/4, rhodium-plated, fausses cotes decoration, 41 jewels, straight line lever escapement, Gyromax balance adjusted to heat, cold, isochronism and 5 positions, shock absorber, self-compensating free-sprung flat balance spring, handengraved skeletonized rotor with 21K gold segment. Dial, case and movement signed. Diam. 39 mm. Thickness 12 mm.
| Grading System | |
|---|---|
Grade: AAA |
Excellent |
Case: 2 |
Very good |
Movement: 2* |
Very good Overhaul recommended, at buyer's expense |
Dial: 1-01 |
As new HANDS Original |
Notes
Equation of Time due to Obliquity (the Earth's tilt). If the Earth's rotational axis was not tilted with respect to its orbit around the Sun, the apparent motion of the Sun along the Ecliptic would fall directly on the Equator, covering the same angles along the Equator in equal time. However, this is not the case, since the angular movement is not linear in terms of time because it changes as the Sun moves above and below the Equator. The projection of the Sun's motion onto the Equator will be at a maximum when its motion along the Ecliptic is parallel to the Equator (at the summer and winter solstices) and will be at a minimum at the equinoxes.
Equation of Time due to Unequal Motion (the Earth's elliptical orbit). The orbit of the Earth around the Sun is an ellipse. The distance between the Earth and the Sun is at a minimum around December 31 and is greatest around July 1. The Sun's apparent longitude changes fastest when the Earth is closest to the Sun. The Sun will appear on the meridian at noon on these two dates and so the Equation of Time due to Unequal Motion will then be zero. The mean solar day, calculated by averaging all the days of the year, was invented by astronomers for convenience so that the solar day would always be 24 hours. True solar time and mean solar time coincide four times a year, on April 16, June 14, September 1, and December 25. On these days, the equation will equal zero. During the other 361 days, the equation of time must be used to indicate the difference between the two times, amounting over 16 minutes at certain times of year. The minimum difference occurs on November 1 with a loss of 16 minutes and 23 seconds and the maximum occurs on February 11 with an increase of 14 minutes 20 seconds. This positive and negative value is offset in the time of the local noon and those of sunrise and sunset. Equation of time, often represented by a figure eight, called an ?analemma?, can be approximated by the following formula: E = 9.87 * sin (2B) ? 7.53 * cos (B) ? 1.5 * sin (B) Where: B = 360 * (N-81) / 365 Where: N = day number, January 1 = day 1.