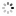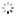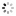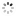Important Collectors Wristwatches, P...
Geneva, Hotel Du Rhone, Apr 02, 2006
LOT 365
?Precision Timekeeper with Equation of Time? Le Roy & Fils. Made circa 1820. Very fine and extremely rare, month?going, weight-driven, mahogany floor-standing regulator with dead-center seconds, equation of time, annual calendar, power reserve indicator and one-second beating grid-iron pendulum.
CHF 80,000 - 120,000
108 50,000 - 77,000
Sold: CHF 118,000
C. Mahogany, ?Empire?, flat pediment above a moulded and stepped cornice, rectangular body with glazed sides and hinged and sprung glazed door with a lock, panelled plinth with concave mouldings and stepped base, the weight concealed within a channel between the backboard of the case and the outer back, two rear doors providing access. D. 18.5 cm., white enamel, convex with radial Roman numerals, inner hour track with 12- minute divisions, outer minute and seconds track, gilt bronze bezel engine turned and finely chased with stiff-leaf decoration. Gilt brass hour and minute hands, blued steel seconds and solar time hands. Brass aperture beneath the dial with silvered annual calendar dial calibrated for the months and their respective symbols, Arabic 10-day numerals, baton 5-day markers and dot date markers. M. Rectangular, gilt brass, arch-top, massive, four massive cylindrical pillars and secured to the gilt brass backplate by four further pillars, with pulley and massive arch-top flat weight set outside and wound through an intermediate gear through the great wheel, providing drive directly to the great wheel mounted at the top of the movement, 5-wheel train, Harrison?s maintaining power, Graham dead-beat escapement with micrometric depth adjustment and micrometric beat adjustment on the crutch, 9-rod brass-iron gridiron pendulum with very heavy bob and micrometric adjustment, knife-edge suspension set on a bracket mounted directly to the back plate panel, power reserve indicator with gilt brass arrow hand. The equation hand and calendar driven from the hour wheel and geared to the equation cam, a roller traces the outline of the cam and drives a rack and pinion which automatically sets the solar time hand to the correct time difference to meantime. Dial signed. Dim. 206 x 49 x 29 cm.
| Grading System | |
|---|---|
Grade: |
|
Case: 3 |
Good |
Movement: 3* |
Good Overhaul recommended, at buyer's expense |
Dial: 3-01 |
Good HANDS Original |
Notes
Indicates the time difference between the true solar day and the mean solar day (or time told by a clock or watch). It has two major causes. The first is that the plane of the Earth's Equator is inclined to Earth?s orbital plane. The second is that the orbit of the Earth around the Sun is an ellipse and not a circle.
Equation of Time due to Obliquity (the Earth's tilt).
If the Earth's rotational axis was not tilted with respect to its orbit around the Sun, the apparent motion of the Sun along the Ecliptic would fall directly on the Equator, covering the same angles along the Equator in equal time. However, this is not the case, since the angular movement is not linear in terms of time because it changes as the Sun moves above and below the Equator. The projection of the Sun's motion onto the Equator will be at a maximum when its motion along the Ecliptic is parallel to the Equator (at the summer and winter solstices) and will be at a minimum at the equinoxes.
Equation of Time due to Unequal Motion (the Earth's elliptical orbit).
The orbit of the Earth around the Sun is an ellipse. The distance between the Earth and the Sun is at a minimum around December 31 and is greatest around July 1. The Sun's apparent longitude changes fastest when the Earth is closest to the Sun. The Sun will appear on the meridian at noon on these two dates and so the Equation of Time due to Unequal Motion will then be zero. The mean solar day, calculated by averaging all the days of the year, was invented by astronomers for convenience so that the solar day would always be 24 hours. True solar time and mean solar time coincide four times a year, on April 16, June 14, September 1, and December 25. On these days, the equation will equal zero. During the other 361 days, the equation of time must be used to indicate the difference between the two times, amounting over 16 minutes at certain times of year. The minimum difference occurs on November 1 with a loss of 16 minutes and 23 seconds and the maximum occurs on February 11 with an increase of 14 minutes 20 seconds. This positive and negative value is offset in the time of the local noon and those of sunrise and sunset. Equation of time, often represented by a figure eight, called an ?analemma?, can be approximated by the following formula: E = 9.87 * sin (2B) ? 7.53 * cos (B) ? 1.5 * sin (B) Where: B = 360 * (N-81) / 365 Where: N = day number, January 1 = day 1.